Форд беллман блок схема

Алгоритм Беллмана-Форда

Алгоритм Беллмана-Форда
Последовательный алгоритм
Последовательная сложность	[math]O(|V||E|)[/math]
Объём входных данных	[math]O(|V| + |E|)[/math]
Объём выходных данных	[math]O(|V|^2)[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]N/A, max O(|V|) [/math]
Ширина ярусно-параллельной формы	[math]O(|E|)[/math]

Содержание

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Алгоритм Беллмана-Форда [1] [2] [3] предназначен для решения задачи поиска кратчайшего пути на графе. Для заданного ориентированного взвешенного графа алгоритм находит кратчайшие расстояния от выделенной вершины-источника до всех остальных вершин графа. Алгоритм Беллмана-Форда масштабируется хуже других алгоритмов решения указанной задачи (сложность [math]O(|V||E|)[/math] против [math]O(|E| + |V|\ln(|V|))[/math] у алгоритма Дейкстры), однако его отличительной особенностью является применимость к графам с произвольными, в том числе отрицательными, весами.

1.2 Математическое описание алгоритма

Пусть задан граф [math]G = (V, E)[/math] с весами рёбер [math]f(e)[/math] и выделенной вершиной-источником [math]u[/math] . Обозначим через [math]d(v)[/math] кратчайшее расстояние от источника [math]u[/math] до вершины [math]v[/math] .

Алгоритм Беллмана-Форда ищет функцию [math]d(v)[/math] как единственное решение уравнения

с начальным условием [math]d(u) = 0[/math] .

1.3 Вычислительное ядро алгоритма

Основной операцией алгоритма является релаксация ребра: если [math]e = (w, v) \in E[/math] и [math]d(v) \gt d(w) + f(e)[/math] , то производится присваивание [math]d(v) \leftarrow d(w) + f(e)[/math] .

1.4 Макроструктура алгоритма

Алгоритм последовательно уточняет значения функции [math]d(v)[/math] .

• В самом начале производится присваивание [math]d(u) = 0[/math] , [math]d(v) = \infty[/math] , [math]\forall v \ne u[/math] .
• Далее происходит [math]|V|-1[/math] итерация, в ходе каждой из которых производится релаксация всех рёбер графа.

Структуру можно описать следующим образом:

1. Инициализация: всем вершинам присваивается предполагаемое расстояние [math]t(v)=\infty[/math] , кроме вершины-источника, для которой [math]t(u)=0[/math] .

2. Релаксация множества рёбер [math]E[/math]

а) Для каждого ребра [math]e=(v,z) \in E[/math] вычисляется новое предполагаемое расстояние [math]t^’ (z)=t(v)+ w(e)[/math] .

б) Если [math]t^’ (z)\lt t(z)[/math] , то происходит присваивание [math]t(z) := t’ (z)[/math] (релаксация ребра [math]e[/math] ).

3. Алгоритм производит релаксацию всех рёбер графа до тех пор, пока на очередной итерации происходит релаксация хотя бы одного ребра.

Если на [math]|V|[/math] -й итерации всё ещё производилась релаксацию рёбер, то в графе присутствует цикл отрицательной длины. Ребро [math]e=(v,z)[/math] , лежащее на таком цикле, может быть найдено проверкой следующего условия (проверяется для всех рёбер за линейное время): [math]t(v)+w(e)\lt d(z)[/math]

1.5 Схема реализации последовательного алгоритма

Последовательный алгоритм реализуется следующим псевдокодом:

1.6 Последовательная сложность алгоритма

Алгоритм выполняет [math]|V|-1[/math] итерацию, на каждой из которых происходит релаксация [math]|E|[/math] рёбер. Таким образом, общий объём работы составляет [math]O(|V||E|)[/math] операций.

Константа в оценке сложности может быть уменьшена за счёт использования следующих двух стандартных приёмов.

1. Если на очередной итерации не произошло ни одной успешной релаксации, то алгоритм завершает работу.
2. На очередной итерации рассматриваются не все рёбра, а только выходящие из вершин, для которых на прошлой итерации была выполнена успешная релаксация (на первой итерации – только рёбра, выходящие из источника).

1.7 Информационный граф

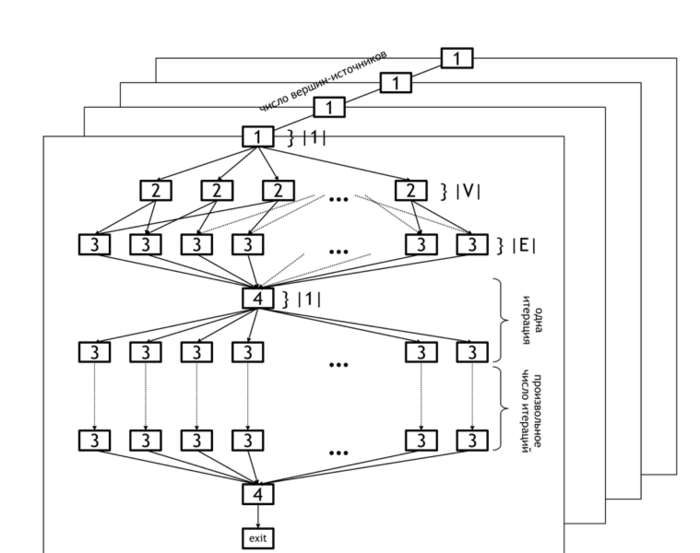
На рисунке 1 представлен информационный граф алгоритма, демонстрирующий описанные уровни параллелизма.

На приведенном далее информационном графе нижний уровень параллелизма обозначен в горизонтальных плоскостях. Множество всех плоскостей представляет собой верхний уровень параллелизма (операции в каждой плоскости могут выполняться параллельно).

Нижний уровень параллелизма на графе алгоритма расположен на уровнях [2] и [3], соответствующим операциям инициализации массива дистанций [2] и обновления массива c использованием данных массива ребер [3]. Операция [4] — проверка того, были ли изменения на последней итерации и выход из цикла, если таковых не было.

Верхний уровень параллелизма, как уже говорилось, заключается в параллельном подсчете дистанций для различных вершин-источников, и на рисунке отмечен разными плоскостями.

1.8 Ресурс параллелизма алгоритма

Алгоритм обладает значительным ресурсом параллелизма. Во-первых, поиск кратчайших путей от различных вершин может производиться независимо для каждой из вершин (параллельные вертикальные плоскости на рисунке 1). Во-вторых, поиск кратчайших путей от фиксированной вершины [math]u[/math] также может выполняться параллельно: инициализация начальных путей [2] требует [math]|V|[/math] параллельных операции, релаксация каждого ребра требует [math]O(|E|)[/math] параллельных операции.

Таким образом, при наличии [math]O(|E|)[/math] процессоров алгоритм завершит работу максимум за [math]|V|[/math] шагов. В реальности, шагов обычно требуется меньше, а именно [math]O(r)[/math] -(максимальная длина среди всех кратчайших путей от выбранной вершины-источника [math]u[/math] ).

Таким образом, ширина ярусно-параллельной формы алгоритма равна [math]O(|E|)[/math] , высота ЯПФ — [math]O(r) | r \lt |V|[/math] .

Алгоритм Δ-шагания может рассматриваться как параллельная версия алгоритма Беллмана-Форда.

1.9 Входные и выходные данные алгоритма

Входные данные: взвешенный граф [math](V, E, W)[/math] ( [math]|V|[/math] вершин [math]v_i[/math] и [math]|E|[/math] рёбер [math]e_j = (v^<(1)>_, v^<(2)>_)[/math] с весами [math]f_j[/math] ), вершина-источник [math]u[/math] .

Объём входных данных: [math]O(|V| + |E|)[/math] .

Выходные данные (возможные варианты):

1. для каждой вершины [math]v[/math] исходного графа – последнее ребро [math]e^*_v = (w, v)[/math] , лежащее на кратчайшем пути от вершины [math]u[/math] к [math]v[/math] , или соответствующая вершина [math]w[/math] ;
2. для каждой вершины [math]v[/math] исходного графа – суммарный вес [math]f^*(v)[/math] кратчайшего пути от от вершины [math]u[/math] к [math]v[/math] .

Объём выходных данных: [math]O(|V|)[/math] .

1.10 Свойства алгоритма

Алгоритм может распознавать наличие отрицательных циклов в графе. Ребро [math]e = (v, w)[/math] лежит на таком цикле, если вычисленные алгоритмом кратчайшие расстояния [math]d(v)[/math] удовлетворяют условию

[math] d(v) + f(e) \lt d(w), [/math]

где [math]f(e)[/math] – вес ребра [math]e[/math] . Условие может быть проверено для всех рёбер графа за время [math]O(|E|)[/math] .

Источник статьи: http://algowiki-project.org/ru/%D0%90%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC_%D0%91%D0%B5%D0%BB%D0%BB%D0%BC%D0%B0%D0%BD%D0%B0-%D0%A4%D0%BE%D1%80%D0%B4%D0%B0

Алгоритм Форда-Беллмана

Задача:

Для заданного взвешенного графа [math]G = (V, E)[/math] найти кратчайшие пути из заданной вершины [math] s [/math] до всех остальных вершин. В случае, когда в графе [math]G[/math] содержатся отрицательные циклы, достижимые из [math]s[/math] , сообщить, что кратчайших путей не существует.

Содержание

Введение [ править ]

Количество путей длины [math]k[/math] рёбер можно найти с помощью метода динамического программирования.
Пусть [math]d[k][u][/math] — количество путей длины [math]k[/math] рёбер, заканчивающихся в вершине [math]u[/math] . Тогда [math] d[k][u] = \sum\limits_ d[k-1][v] [/math] .

Аналогично посчитаем пути кратчайшей длины. Пусть [math]s[/math] — стартовая вершина. Тогда [math] d[k][u] = \min\limits_(d[k-1][v] \: + \: \omega(u, v))[/math] , при этом [math]d[0][s] = 0[/math] , а [math]d[0][u] = +\infty [/math]

Доказательство: [math]\triangleright[/math] Пусть кратчайший путь состоит из [math]k[/math] ребер, тогда корректность формулы следует из динамики, приведенной ниже. [math]\triangleleft[/math]

Псевдокод [ править ]

Используя приведенные формулы, алгоритм можно реализовать методом динамического программирования.

Также релаксацию можно свести к одномерному случаю, если не хранить длину пути в рёбрах. Одномерный массив будем обозначать [math]d'[/math] , тогда [math]d'[u] = \min(d'[u], \; d'[v] + \omega(vu))[/math]

Корректность [ править ]

Доказательство: [math]\triangleright[/math]

Воспользуемся индукцией по [math]k[/math] :

При [math]k = 0[/math] выполнено: [math]\rho(s, u) \leqslant +\infty \leqslant +\infty [/math]

Сначала докажем, что [math] \rho(s, u) \leqslant d'[u][/math] . Пусть после [math]k — 1 [/math] итерации выполняется [math]\rho(s, u) \leqslant d'[u] \leqslant \min\limits_ d[i][u][/math] для всех [math]u[/math] . Тогда после [math]k[/math] итераций [math] \rho(s, v) = \min\limits_ (\rho(s, u) + \omega(uv)) \leqslant \min\limits_ (d'[u] + \omega(uv)) = d'[v][/math] .

Переходим ко второму неравенству. Теперь возможно два случая:

1. [math]\min\limits_ d[i][u] = d[k+1][u][/math]
2. [math]\min\limits_ d[i][u] = d[j][u] =\min\limits_ \; d[i][u][/math]

Рассмотрим 1 случай: [math]\min\limits_ d[i][u] = d[k+1][u][/math]
[math]d'[u] \leqslant d'[v] + \omega(vu) \leqslant d[k][v] + \omega(vu) = d[k+1][u][/math] 2 случай расписывается аналогично. Таким образом переход выполнен и [math]\rho(s, u) \leqslant d'[u] \leqslant \min\limits_ d[i][u][/math] выполняется. [math]\triangleleft[/math]

Реализация алгоритма и ее корректность [ править ]

В этом алгоритме используется релаксация, в результате которой [math]d[v][/math] уменьшается до тех пор, пока не станет равным [math]\delta(s, v)[/math] . [math]d[v][/math] — оценка веса кратчайшего пути из вершины [math]s[/math] в каждую вершину [math]v \in V[/math] .
[math]\delta(s, v)[/math] — фактический вес кратчайшего пути из [math]s[/math] в вершину [math]v[/math] .

Доказательство: [math]\triangleright[/math]

Рассмотрим произвольную вершину [math]v[/math] , достижимую из [math]s[/math] . Пусть [math]p = \langle v_0. v_ \rangle [/math] , где [math]v_0 = s[/math] , [math]v_ = v[/math] — кратчайший ациклический путь из [math] s [/math] в [math] v [/math] . Путь [math] p [/math] содержит не более [math] |V| — 1 [/math] ребер. Поэтому [math]k \leqslant |V| — 1[/math] .

Докажем следующее утверждение:

После [math]n : (n \leqslant k)[/math] итераций первого цикла алгоритма, [math]d[v_n] = \delta(s, v_n) [/math]

Воспользуемся индукцией по [math]n[/math] :

Перед первой итерацией утверждение очевидно выполнено: [math]d[v_0] = d[s] = \delta(s, s) = 0[/math]

Пусть после [math]n : (n \lt k)[/math] итераций, верно что [math]d[v_n] = \delta(s, v_n)[/math] . Так как [math](v_n, v_)[/math] принадлежит кратчайшему пути от [math]s[/math] до [math]v[/math] , то [math]\delta(s, v_) = \delta(s, v_n) + \omega(v_n, v_)[/math] . Во время [math]l + 1[/math] итерации релаксируется ребро [math](v_n,v_)[/math] , следовательно по завершению итерации будет выполнено [math]d[v_] \leqslant d[v_n] + \omega(v_n, v_) = \delta(s, v_n) + \omega(v_n, v_) = \delta(s, v_)[/math] . Ясно, что [math]d[v_] \geqslant \delta(s, v_) [/math] , поэтому верно что после [math]l + 1[/math] итерации [math]d[v_] = \delta(s, v_)[/math] . Индукционный переход доказан. Итак, выполнены равенства [math]d[v] = d[v_] = \delta (s, v_) = \delta (s, v)[/math] . [math]\triangleleft[/math]

Теорема:

Доказательство:

[math]\triangleright[/math]

Пусть граф [math] G [/math] не содержит отрицательных циклов, достижимых из вершины [math] s [/math] . Тогда если вершина [math] v [/math] достижима из [math] s [/math] , то по лемме [math] d[v] = \delta (s, v)[/math] . Если вершина [math] v [/math] не достижима из [math] s [/math] , то [math] d[v] = \delta (s, v) = \mathcal <1>[/math] из несуществования пути. Теперь докажем, что алгоритм вернет значение [math] true [/math] . После выполнения алгоритма верно, что для всех [math] (u, v) \in E, \ d[v] = \delta (s, v) \leqslant \delta (s, u) + \omega (u,v) = d[u] + \omega (u,v)[/math] , значит ни одна из проверок не вернет значения [math] false [/math] . Пусть граф [math] G [/math] содержит отрицательный цикл [math] c = > [/math] , где [math] v_0 = v_ [/math] , достижимый из вершины [math] s [/math] . Тогда [math]\sum\limits_^ <\omega (v_, v_)> \lt 0 [/math] . Предположим, что алгоритм возвращает [math] true [/math] , тогда для [math] i = 1. k [/math] выполняется [math] d[v_] \leqslant d[v_] + \omega (v_, v_) [/math] . Просуммируем эти неравенства по всему циклу: [math]\sum\limits_^ ]> \leqslant \sum\limits_^ ]> + \sum\limits_^ <\omega (v_, v_)> [/math] . Из того, что [math] v_0 = v_ [/math] следует, что [math] \sum\limits^_ ]> = \sum \limits_^ ]> [/math] . Получили, что [math] \sum \limits_^ <\omega (v_, v_)> \geqslant 0 [/math] , что противоречит отрицательности цикла [math] c [/math] .

[math]\triangleleft[/math]

Сложность [ править ]

Инициализация занимает [math] \Theta (V) [/math] времени, каждый из [math] |V| — 1 [/math] проходов требует [math] \Theta (E) [/math] времени, обход по всем ребрам для проверки наличия отрицательного цикла занимает [math]O(E)[/math] времени. Значит алгоритм Беллмана-Форда работает за [math]O(V E)[/math] времени.

Нахождение отрицательного цикла [ править ]

Приведенная выше реализация позволяет определить наличие в графе цикла отрицательного веса. Чтобы найти сам цикл, достаточно хранить вершины, из которых производится релаксация.

Если после [math]|V| — 1[/math] итерации найдется вершина [math] v [/math] , расстояние до которой можно уменьшить, то эта вершина либо лежит на каком-нибудь цикле отрицательного веса, либо достижима из него. Чтобы найти вершину, которая лежит на цикле, можно [math]|V| — 1[/math] раз пройти назад по предкам из вершины [math] v [/math] . Так как наибольшая длина пути в графе из [math]|V|[/math] вершин равна [math]|V| — 1[/math] , то полученная вершина [math] u [/math] будет гарантированно лежать на отрицательном цикле.

Зная, что вершина [math] u [/math] лежит на цикле отрицательного веса, можно восстанавливать путь по сохраненным вершинам до тех пор, пока не встретится та же вершина [math] u [/math] . Это обязательно произойдет, так как в цикле отрицательного веса релаксации происходят по кругу.

Источник статьи: http://neerc.ifmo.ru/wiki/index.php?title=%D0%90%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC_%D0%A4%D0%BE%D1%80%D0%B4%D0%B0-%D0%91%D0%B5%D0%BB%D0%BB%D0%BC%D0%B0%D0%BD%D0%B0