Работа силы тяги двигателя при движении автомобиля

Как найти силу тяги

Что такое сила тяги

Сила тяги — сила, прикладываемая к телу для поддержания его в постоянном движении.

Действие силы тяги

Множество сил, действующих на движущийся объект, для упрощения вычислений делят на две группы: силу тяги и силы сопротивления.

Её прекращение

Когда действие силы тяги прекращается, движущееся тело замедляется и постепенно останавливается, так как на него воздействуют силы, мешающие продолжать двигаться, например, трение.

1 закон Ньютона о действии

Согласно этому закону в формулировке самого Ньютона, любое тело остается в покое или равномерно движется по прямой, пока на него не воздействуют силы, заставляющие его изменить это состояние.

В современной физике в формулировку внесены уточнения:

• закон применим только в системах отсчета, называемых инерциальными;
• тело может вращаться на месте, не находясь под воздействием внешних сил, поэтому вместо термина «тело» следует использовать термин «материальная точка».

Чтобы переместить неподвижный предмет, на него должна воздействовать некая сила. Чтобы изменить скорость движения предмета, также необходимо воздействие силы, замедляющей его или ускоряющей. Так как предметы обладают разной массой и соответственно разной инертностью, силы, достаточные для эффективного воздействия, тоже будут различаться.

Состояние ускорения после воздействия силы тяги

Когда движение равномерное, сила тяги и сила трения совершают одинаковую работу, уравновешивая друг друга. Воздействие силы на тело в направлении движения придает ему ускорение. Если направить ту же силу в противоположном направлении, она замедлит движение тела, что можно назвать отрицательным ускорением.

Формулы для определения силы тяги

Согласно второму закону Ньютона, сумма сил, воздействующих на движущееся тело, равна массе \(m\) , умноженной на ускорение \(a\) . Универсальной формулы, подходящей для любого сочетания сил, не существует. Чаще всего силу тяги находят с помощью общей формулы \( F_т-\;F_<с>=m\;\times\;a\) , где \(F_т\) — сила тяги, \(F_<с>\) — силы сопротивления.
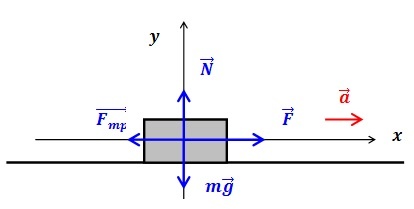
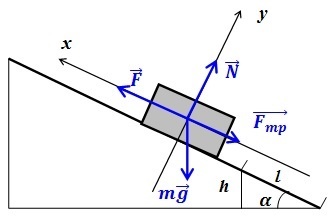
При решении конкретной задачи силы, воздействующие на тело, схематически изображают в виде векторов. На схеме:

• сила тяжести mg;
• сила реакции опоры \(N\) ;
• сила трения \( F_<тр>\) ;
• сила тяги \(F\) .

При нахождении тела на горизонтальной поверхности сила тяжести и сила реакции опоры уравновесят друг друга. Но если транспортное средство движется в гору или под гору, придется учесть влияние уклона. Тогда формула может выглядеть так: \(F_т-\;F_с-\;mg\;\times\;\sin\alpha=m\;\times\;a.\)

Работа A, которую должна совершить сила тяги, сдвигая тело, связана с ней соотношением \(A\;=\;F\;\times\;s\) . \(s\) здесь — расстояние, на которое тело переместилось.

Какое условие должно соблюдаться

Сила тяги всегда должна быть больше противодействующих ей сил.

Формула через мощность

Полезную механическую мощность \(N\) можно вычислить по формуле \(N=F_т\;\times\;v\) , где \(v\) — скорость. Для определения силы тяги нужно разделить мощность на скорость: \(F_т\;=\;\frac N v.\)

Измерение и обозначение силы тяги

Силу тяги обозначают \(F_т\) или \(F\) . Единица измерения — ньютон ( \(Н\) ).
Для решения задач недостаточно измерить усилие, приложенное к объекту, и выразить его конкретным числом, так как сила обладает еще и направлением. Чтобы подчеркнуть, что сила — векторная величина, к буквенному обозначению добавляют стрелку.

Как определить силу тяги двигателя. Примеры решения задач

Задача 1

Автомобиль может разгоняться до 216 км/ч. Максимальная мощность двигателя равна 96 кВт. Определите максимальную силу тяги двигателя.

Решение

Переведем киловатты в ватты, а километры в час — в метры в секунду:

\(F_т\;=\;\frac N v = \frac<96000> <60>= 1600 Н\)

Задача 2

Троллейбус весом 12 тонн за 5 секунд проезжает по горизонтальной дороге 10 метров. Сила трения равна 2,4 кН. Определите силу тяги, которую развивает двигатель.

Решение

Переведем тонны в килограммы, а килоньютоны в ньютоны:

\(F_т-\;F_<тр>=m\;\times\;a\) , следовательно, \(F_т=m\times a\;+\;F_<тр>\)

Чтобы определить ускорение а, воспользуемся формулой \(s\;=\;\frac2\)

Подставив численные значения величин, получаем:

Задача 3

Транспорт, весящий 4 тонны, едет в гору. Уклон — 1 метр на каждые 25 метров пути. \(\mu\) — 0,1 от силы тяжести, \(а = 0\) . Определите силу тяги.

Решение

Сделаем проекции на координатные оси:

Подставим значение \(F_<тр>\) в уравнение \(OX\) и определим \(F_т\) :

Найдем синус и косинус \(\alpha\) , подставим их в общую формулу:

Нужно подобрать материалы для студенческой работы?

Источник статьи: http://wiki.fenix.help/fizika/sila-tyagi

Устройство автомобилей

Основы динамики автомобиля

Скоростная характеристика двигателя

Скоростная характеристика двигателя определяется зависимостями эффективной мощности N_e и крутящего момента M_к от частоты вращения n коленчатого вала.

Ведущие колеса автомобиля приводят его в движение в результате возникновения силы тяги, которая возникает при приложении крутящего момента к полуосям ведущих колес со стороны трансмиссии:

где P_т – сила тяги, Н;
M_т – крутящий (тяговый) момент на ведущем колесе, Нм;
r – радиус колеса, м.

Крутящий момент на ведущих колесах зависит от величины момента, развиваемого двигателем на коленчатом валу, передаточного числа i_тр трансмиссии и ее КПД – η_тр :

Сила тяги P_т на ведущих колесах может быть определена не только по формуле (1), но и с учетом скорости v_i движения автомобиля на i -й передаче и развиваемой двигателем эффективной мощности N_е :

Скорость v_i движения автомобиля на i -й передаче пропорциональна частоте n вращения коленчатого вала, радиусу r ведущего колеса и обратно пропорциональна передаточному числу i_тр i трансмиссии на i -й передаче:

Таким образом, частота вращения n коленчатого вала является определяющим параметром для показателей эффективной мощности N_е , крутящего момента M_к и силы тяги на ведущих колесах P_т .

На рисунке 1 приведена внешняя скоростная характеристика двигателя при полностью открытой дроссельной заслонке, которая определяет предельные возможности двигателя при значениях частоты вращения коленчатого вала от n_min до n_max .

Анализ графика показывает, что максимальная эффективная мощность и максимальный крутящий момент, развиваемый двигателем, доступен в узком интервале частот вращения коленчатого вала. При небольшой частоте вращения коленчатого вала величина этих динамических показателей недостаточна для появления на ведущих колесах требуемой для движения автомобиля силы тяги, а при превышении частотой вращения коленвала некоторого максимального порога двигатель начинает терять мощность и тяговые показатели, или, как говорят механики, начинает работать «вразнос».
По этой причине эффективная эксплуатация двигателя внутреннего сгорания возможна лишь в некотором узком диапазоне частот вращения коленчатого вала.

Скоростная характеристика двигателя во многом зависит от типа двигателя: чем круче кривая эффективной мощности N_е , тем большей приемистостью обладает двигатель.

Тяговая характеристика автомобиля

Тягово-скоростные свойства автомобиля удобно оценивать с помощью тяговой характеристики, т. е. зависимостью силы тяги на ведущих колесах от скорости движения на различных передачах (рис. 2).

Используя скоростную характеристику и задавая частоты вращения коленчатого вала от n_min до n_max при соответствующих значениях эффективной мощности или крутящего момента для каждой передачи по формуле (4) находят значения скорости v , а по формуле (3) находят значение тяговой силы P_т .

Число кривых на тяговой характеристике (рис. 2) соответствует числу ступеней в коробке передач.

Тяговая характеристика позволяет быстро определить максимальное значение силы тяги на ведущих колесах, которая может быть обеспечена при данной скорости движения автомобиля, поскольку она рассчитывается по наибольшей для данной частоты вращения коленчатого вала мощности двигателя. Меньшее значение силы тяги получается при недоиспользовании мощности двигателя, т. е. при неполной подаче топлива. Следовательно, с помощью тяговой характеристики можно оценить предельные тяговые возможности автомобиля в фактическом интервале скоростей его движения.

Силы и моменты, действующие на ведущие колеса

На ведущие колеса автомобиля действуют силы со стороны автомобиля (т. е. со стороны двигателя посредством агрегатов трансмиссии), а также силы со стороны дороги. Обозначим силы, действующие со стороны автомобиля, буквой Р , а со стороны дороги – буквой R (рис. 3).

Реактивные силы, действующие на колеса

Тяговый момент М_т на ведущих колесах стремится сдвинуть назад верхний слой дорожного покрытия, в результате чего со стороны дороги на ведущее колесо в зоне контакта действует противоположно направленная сила R_x – горизонтально направленная касательная реакция дороги.

Так как на автомобиле используются эластичные пневматические шины, то неизбежна частичная потеря момента М_т , поэтому продольную (горизонтальную) реакцию со стороны дороги, обеспечивающую качение колеса, можно записать как разность между силой тяги и потерями в шине:

где Р_ш – сила, учитывающая потери энергии в шинах ведущих колес.

Таким образом, касательная реакция дороги создает силу тяги.

Автомобиль своим весом G действует на каждое колесо, передавая усилие на дорогу, и, соответственно, вызывая нормальную реакцию дороги R_z . Следует учитывать, что при наличии на колесе крутящего момента нормальная реакция R_z прикладывается не к оси симметрии опорной площадки колеса, а на некотором расстоянии α_ш от нее, поскольку имеет место смещение центра давления из-за эластичности шины.

Эпюра элементарных нормальных реакций дороги, показанная на рисунке 4, объясняет причину смещения точки приложения реакции R_z . Это происходит из-за того, что нормальные реакции на переднем и заднем участках опорной площадки колеса различны по величине, так как силы, возникающие в упругом материале шины при приложении и снятии нагрузки неодинаковы.
Это объясняется действием сил внутреннего трения между взаимно перемещающимися частицами материала шины. При приложении нагрузки эти силы и силы упругости направлены в одну и ту же сторону, а при снятии – в противоположные стороны.

Боковая сила Р_y значительно увеличивается при криволинейном движении автомобиля или при движении по косогору. Боковая реакция R_y со стороны дороги удерживает колеса автомобиля от бокового скольжения (заноса) при движении автомобиля поперек косогора или при выполнении маневра.

Сила тяги на ведущих колесах

Сила тяги Р_т на ведущих колесах может быть определена, как отношение крутящего (тягового) момента M_т , подводимого к колесам, к их радиусу r :

При этом не учитываются затраты энергии на деформацию дорожного покрытия, трение внутри шины и силы инерции, обусловленные ускорением вращающихся масс колес и деталей трансмиссии в случае неравномерного движения.

Следует учитывать, что радиус колеса вследствие эластичности шины является переменной величиной.
Различают следующие радиусы автомобильных колес:

• статический радиус колеса r_ст – расстояние от поверхности дороги до оси неподвижного колеса, воспринимающего вертикальную нагрузку, обусловленную силой тяжести, действующей на автомобиль (т. е. его весом G ). Значения статического радиуса приводятся заводом-изготовителем шины в технических характеристиках;
• динамический радиус колеса r_д – расстояние от поверхности дороги до оси катящегося колеса. Динамический радиус колеса во время движения может превышать его статический радиус, поскольку в результате нагрева шины давление внутри нее увеличивается.
  Кроме того, под действием центробежных сил с возрастанием скорости автомобиля шина растягивается в радиальном направлении, вследствие чего динамический радиус увеличивается. Динамический радиус, также, зависит от величины вертикальной нагрузки P_z .
• радиус качения колеса r_к – радиус условного недеформирующегося катящегося без скольжения колеса, которое имеет с данным эластичным колесом одинаковую угловую и линейную скорости.

Радиус качения колеса определяется по формуле:

где S – путь, пройденный колесом; n_к – число оборотов колеса на пути S .

Если проскальзывание колеса относительно дороги отсутствует, что характерно для ведомого колеса, то радиусы r_д и r_к почти равны между собой. В случае полного буксования колеса его пройденный путь будет равен нулю, и тогда (согласно приведенной выше формуле) его радиус качения тоже будет равен нулю.
В случае движения колеса юзом (скольжение без вращения) число оборотов будет равно нулю, и, соответственно, радиус качения r_к будет стремиться к бесконечности.

Различают еще и свободный радиус колеса r_св , который является половиной диаметра ненагруженного колеса при отсутствии его контакта с опорной поверхностью.

На дорогах с сухим покрытием скольжение ведущих колес и изменение радиуса незначительны. Поэтому радиусы статический r_ст , динамический r_д и качения r_к при расчетах считаются одинаковыми и обозначаются буквой r .

Источник статьи: http://k-a-t.ru/PM.01_mdk.01.01/7_teoria_avto_3/index.shtml

Учебники

Журнал «Квант»

Общие

Черноуцан А.И. Кое-что о силе тяги //Квант. — 1992. — № 5. — С. 42-44.

По специальной договоренности с редколлегией и редакцией журнала «Квант»

В задачах по механике, особенно из раздела «Механическая мощность», часто встречается величина, называемая силой тяги — поезда, автомобиля, самолета, велосипеда и т. п. Что это за сила? Какова ее природа?

Иногда можно услышать ответ, что, поскольку автомобиль, например, приводится в движение двигателем, то и сила тяги действует со стороны двигателя. Это, конечно, не так. Внутренние силы, действующие со стороны одной части системы на другую, не могут изменить скорость системы как целого — это противоречило бы закону сохранения импульса. Тогда становится ясно, что надо рассматривать силы, действующие на транспортное средство извне, со стороны внешнего мира. Так, в случае автомобиля или поезда сила тяги — это сила трения покоя, действующая на ведущие колеса со стороны дороги, в случае самолета — сила реакции отбрасываемого назад воздуха. Правда, для того чтобы сила трения покоя была направлена вперед, двигатель должен вращать колеса в нужном направлении, заставляя их как бы цепляться за дорогу и создавать силу тяги. Так что без двигателя действительно далеко не уедешь.

Зачем же вводить некую силу тяги, а не писать прямо «сила трения покоя» или «сила реакции воздуха»? Оказывается, удобно все силы, действующие на транспортное средство со стороны окружающих тел, разделить на две части: одну часть назвать силой тяги F_T, а другую — силой сопротивления F_C. В этом случае, во-первых, приобретают универсальный вид уравнения движения. Так, для автомобиля, поднимающегося в гору с уклоном α, запишем

F_T — F_C — mg \sin \alpha = ma\) . (1)

Во-вторых, через силу тяги весьма просто выражается полезная механическая мощность:

P_0 = F_T \upsilon\) , (2)

где υ — скорость транспортного средства. (Как будет показано дальше, эту формулу можно считать в каком- то смысле определением полезной мощности транспортного средства.) Формулы (1) и (2) вместе позволяют понять многие процессы, происходящие при разгоне или движении транспортных средств.

Например, автомобилисты знают, что при разгоне автомобиля по горизонтальной дороге невыгодно включать большую мощность на малых скоростях. И действительно — когда сила тяги, равная \(

\frac<\upsilon>\), достигнет максимальной силы трения покоя μN, начнется пробуксовка колес, что является крайне нежелательным. А максимальную мощность P_max можно использовать только при достижении скорости \(

\upsilon_0 = \frac><\mu N>\), а до этого мощность надо плавно наращивать. Наверное, большинство из вас все это хорошо понимают и так, и взяться за написание этой заметки меня заставило совсем другое. Дело в том, что формула для полезной мощности (2), соответствуя внешне определению механической мощности и поэтому не привлекая особого внимания, содержит в себе неожиданный парадокс. Должен признаться, что сам я долгое время не обращал на него никакого внимания. В чем же он заключается?

Как уже говорилось, сила тяги автомобиля, например, есть не что иное, как сила трения покоя, приложенная со стороны дороги к нижним точкам ведущих колес. Но эти точки (разумеется, если колеса не проскальзывают) касаются дороги, т. е. имеют скорость, равную нулю. Значит, работа силы трения покоя, а следовательно, и работа силы тяги, равна нулю!

В первый момент, когда я это понял, у меня возникло ощущение легкого испуга. Нет, я не испугался за закон сохранения энергии — энергия совсем не обязательно должна поступать в систему извне. Хотя внутренние силы, возникающие при работе двигателя, не способны изменить импульс системы, они вполне могут изменить ее энергию. Например, если в двигателе используется энергия сгорания топлива, то часть этой энергии при работе двигателя теряется, а часть превращается в полезную механическую энергию. А вот при отсутствии в системе двигателя, поставляющего необходимую энергию, внешняя сила тяги должна быть «устроена» так, чтобы самой совершать работу. (Пример: при буксировке автомобиля с выключенным двигателем роль силы тяги играет сила натяжения троса.)

Неприятность заключалась в другом — универсальная формула (2) потеряла свою очевидность. Стало неясно, можно ли ее в таком простом виде использовать для решения различных задач или придется в каждом случае специально вычислять полезную мощность, опираясь на конкретное устройство двигателя.

Рассмотрим, например, игрушечный автомобиль, где источником энергии является энергия упругой деформации пружины. Для упрощения пренебрежем массой колес и пружины. Полезную работу в этом случае совершает сила, приложенная к корпусу автомобиля, которая равна сумме силы \(

\vec F_0\), действующей на ось колеса, и силы натяжения \(

\vec F_n\) действующей на стенку корпуса; следовательно,

P_0 = (F_0 — F_n) \upsilon\) .

Так как масса колеса равна нулю, сумма всех действующих на него сил равна нулю, т. е.

Поэтому P₀, как и в формуле (2), оказывается равной произведению F_Tυ. В чем же дело? Может быть, это случайность?

Чтобы понять причину такого совпадения, задумаемся о том, что мы называем полезной механической работой при движении транспортного средства любой природы в общем случае. Во-первых, это работа против сил сопротивления \(

A_1 = F_C \Delta l\), во-вторых, работа по увеличению кинетической энергии поступательного движения \(

A_2 = \frac <2>— \frac<2>\) и, в-третьих, работа по изменению потенциальной энергии \(

A_3 = mg \Delta h\). К потерянной энергии относят тепловые потери в механизме, кинетическую энергию вращения колес, движения шатунов, поршней и т. д., другими словами — все, что не входит в энергию поступательного движения транспортного средства как целого.

Теперь — немного математики. Умножим обе части формулы (1) на Δl. Учитывая, что \(

mg \Delta l \sin \alpha = mg \Delta h\), запишем

F_T \Delta l = F_C \Delta l + \left(\frac <2>— \frac <2>\right) + mg \Delta h\) .

Получается, что величина, формально составленная как работа силы тяги F_T на пути Δl (на самом деле сила тяги работы не совершает), в точности равна полезной работе A₁ + A₂ + A₃. Следовательно, полезную мощность можно смело вычислять по формуле (2)!

Итак, мы выяснили, что сила тяги, определенная как внешняя сила, входящая в уравнение движения (1), работы не совершает, так как она приложена к неподвижной точке колеса. Кроме того, та часть работы двигателя, которую называют полезной, равна работе силы тяги, как если бы она была приложена не к неподвижной точке, а к движущемуся корпусу транспортного средства. Но самое главное — мы еще раз убедились в том, что за привычными и обыкновенными, на первый взгляд, понятиями часто скрываются неожиданные вопросы и парадоксы, над которыми полезно и интересно поразмышлять.

Источник статьи: http://www.physbook.ru/index.php/Kvant._%D0%A1%D0%B8%D0%BB%D0%B0_%D1%82%D1%8F%D0%B3%D0%B8